STDEVA

Szacuje odchylenie standardowe oparte na próbce. Odchylenie standardowe pozwala określić, jak dalece wartości odbiegają od wartości średniej. Tekst i wartości logiczne, takie jak PRAWDA i FAŁSZ, są uwzględniane w obliczeniach.

Składnia

STDEVA(wartość1,wartość2, ...)

Wartość1,wartość2, ... są wartościami od 1 do 30, odpowiadającymi próbce populacji.

Spostrzeżenia

Zasad działania funkcji STDEVA opiera się na założeniu, że argumenty tej funkcji są próbką populacji. Jeżeli dane reprezentują całą populację, należy obliczyć odchylenie standardowe za pomocą funkcji STDEVPA.
Argumenty zawierające wartość PRAWDA są interpretowane jako 1; argumenty zawierające tekst lub wartość FAŁSZ są interpretowane jako 0 (zero). Jeżeli w obliczeniach nie można uwzględniać tekstu ani wartości logicznych, należy użyć funkcji arkusza kalkulacyjnego STDEV.
Odchylenie standardowe oblicza się przy użyciu metody „nieobciążonej” lub metody „n-1”.
Formuła funkcji STDEVA jest następująca:

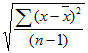
Przykład

Załóżmy, że 10 narzędzi wyprodukowanych za pomocą jednej maszyny w jednym cyklu produkcyjnym stanowi próbkę testowaną pod kątem wytrzymałości na złamanie.

Wyt1	Wyt2	Wyt3	Wyt4	Wyt5	Wyt6	Wyt7	Wyt8	Wyt9	Wyt10	Formuła	Opis (wynik)
1345	1301	1368	1322	1310	1370	1318	1350	1303	1299	=STDEVA([Wyt1], [Wyt2], [Wyt3], [Wyt4], [Wyt5], [Wyt6], [Wyt7], [Wyt8], [Wyt9], [Wyt10])	Odchylenie standardowe wytrzymałości na złamanie wszystkich narzędzi (27,46391572)