STDEV

Szacuje odchylenie standardowe na podstawie próbki. Odchylenie standardowe określa, jak daleko wartości odbiegają od wartości średniej.

Składnia

STDEV(liczba1,liczba2,...)

Liczba1,liczba2,...   są argumentami numerycznymi (od 1 do 30) odpowiadającymi próbce populacji.

Spostrzeżenia

• Wartości logiczne, takie jak PRAWDA i FAŁSZ, oraz tekst są ignorowane. Jeżeli wartości logiczne i tekst nie mogą być ignorowane, należy użyć funkcji STDEVA.
• Działanie funkcji STDEV opiera się na założeniu, że jej argumenty są próbkami populacji. Jeżeli dane reprezentują całą populację, należy obliczyć odchylenie standardowe za pomocą funkcji STDEVP.
• Odchylenie standardowe oblicza się za pomocą metody „nieobciążonej” lub „n-1”.
• Funkcja STDEV wykorzystuje następującą formułę:

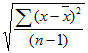
Przykład

Załóżmy, że 10 narzędzi wyprodukowanych w ramach tej samej partii tworzy próbkę losową. Są one badane pod kątem wytrzymałości na złamanie.